Quadratic Forms
Express the polynomial without the cross product terms: 
 , where x is [x_1;x_2,x_3] (in MATLAB notation)
, where x is [x_1;x_2,x_3] (in MATLAB notation)
A = [2 2 0; 2 2 0; 0 0 2];
We want to substitute  so that
so that  is orthogonal. Then, we would get
is orthogonal. Then, we would get  . If we find a
. If we find a  that orthogonally diagonalizes
that orthogonally diagonalizes 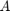 , then
, then 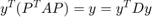 , where
, where 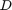 is a matrix with the main diagonal containing eigenvalues of
is a matrix with the main diagonal containing eigenvalues of 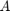 .
.
[P,D] = eig(A)
P =
-0.7071 0 0.7071
0.7071 0 0.7071
0 1.0000 0
D =
0 0 0
0 2 0
0 0 4
We have  . So,
. So,  .
.