Quadratic Forms

Express the polynomial without the cross product terms: 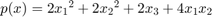$p(x)=2{x_1}^2 + 2{x_2}^2 + 2{x_3} + 4{x_1}{x_2}$

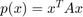$p(x) = x^T A x$ , where x is [x_1;x_2,x_3] (in MATLAB notation)

A = [2 2 0; 2 2 0; 0 0 2];

We want to substitute 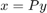$x=Py$ so that 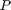$P$ is orthogonal. Then, we would get 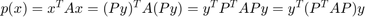$p(x)= x^TAx=(Py)^TA(Py)=y^TP^TAPy=y^T(P^TAP)y$ . If we find a 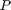$P$ that orthogonally diagonalizes 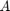$A$ , then 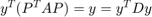$y^T(P^TAP)=y=y^TDy$ , where 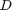$D$ is a matrix with the main diagonal containing eigenvalues of $A$ .

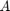[P,D] = eig(A)

P =

   -0.7071         0    0.7071
    0.7071         0    0.7071
         0    1.0000         0


D =

     0     0     0
     0     2     0
     0     0     4

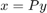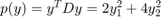We have $x=Py$ . So, $p(y) = y^TDy=2y_1^2+4y_2^2$ .